leetcode373、632 多路归并+堆

leetcode 373

这是一道top k问题，首先从最原始的思路想，可以用双指针暴力枚举所有情况然后取前k个，但这就没有利用好两个数组都是已排序的条件，假设我们已经得到了前n个最小的,那么下一个要考虑的就是这n个数中的每一个的$(a_{i},b{i+1})$和$(a_{i+1},b{i})$中最小的那一个，可以用堆来动态的维护当前的最小值并完成多路归并，这里的多路可能还比较缥缈，先考虑一个可能会重复的问题，很明显a[0]+b[0]是最小的，之后有两条路都可以走到a[1]+b[1]这里导致了重复，所以我们可以先把第一列放入堆里，然后进行按每一路动态的游走，所有路的步数和为k次就停止，可见下图

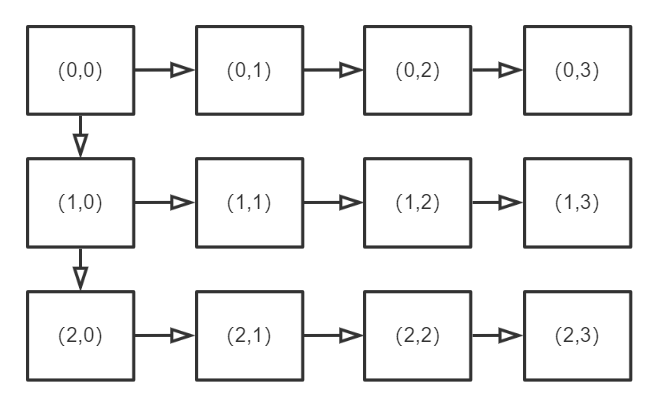
另一个要考虑的问题是，我们堆里存的是索引对，但是是根据数组和来确实排序的，所以要把这些信息都要放进堆里，设计为pair<int, pair<int, int>，即<和，<索引，索引>。

c++

class Solution {
public:
    vector<vector<int>> kSmallestPairs(vector<int>& nums1, vector<int>& nums2, int k) {
        priority_queue<pair<int, pair<int, int>>, vector<pair<int, pair<int, int>>>, greater<pair<int, pair<int, int>>>> heap;
        int m = nums1.size();
        int n = nums2.size();
        for (int i = 0; i < min(m, k); i++) {
            heap.push({nums1[i] + nums2[0], {i, 0}});
        }
        vector<vector<int>> res;
        while (k-- && !heap.empty()) {
            auto p = heap.top();
            heap.pop();
            int a  = p.second.first, b = p.second.second;
            if (b + 1 < n) {
                heap.push({nums1[a]+ nums2[b + 1], {a, b + 1}}); 
            }
            res.emplace_back(initializer_list<int>{nums1[a], nums2[b]});
        }
        return res;
    }
};

还有一种官方题解的方法是用lambda表达式来捕获数组直接完成建堆

c++

auto cmp = [&nums1, &nums2](const pair<int, int> & a, const pair<int, int> & b) {
            return nums1[a.first] + nums2[a.second] > nums1[b.first] + nums2[b.second];
        };
priority_queue<pair<int, int>, vector<pair<int, int>>, decltype(cmp)> pq(cmp);

下面解释一下这个优先队列的用法，
1.为什么用decltype?
优先队列的第三个参是需要指定一个实现了 operator< 操作符的类或者结构体，而lambda是一个值，
2.为什么最后还有吧cmp传入构造函数？
因为lambda没有默认构造函数的（构造函数和赋值运算符删除，拷贝构造和析构隐试定义

c++

struct node {
	int x, y;
	int i, j;
	bool operator < (const node &other) {
		return x + y > other.x + other.y;
	}
}

参考：https://ask.csdn.net/questions/7399659
https://stackoverflow.com/questions/5807735/c-priority-queue-with-lambda-comparator-error
https://stackoverflow.com/questions/41053232/c-stdpriority-queue-uses-the-lambda-expression

leetcode 632

这道题可以理解为是从k个列表中分别取一个数，使得这k个数中的最大值与最小值的差最小。同样利用好每个列表都是非递减排的条件，可以基于贪心的思想，首先给每个列表分配一个指针，起始都指向表头，然后用最小堆维护当前k个数的最小值同时维护当前的最大值，每次移动最小值也就是左边界，直到有某个列表遍历完成
同样采样类似上题的数据结构

Code

class Solution {
public:
    vector<int> smallestRange(vector<vector<int>>& nums) { 
        priority_queue<pair<int, pair<int, int>>, vector<pair<int, pair<int, int>>>, greater<pair<int, pair<int, int>>>> heap;
        int res =  INT_MAX;
        vector<int> ans(2);
        ans[0] = -1;
        int n = nums.size();
        vector<int> index(n);
        int max_value = 0;
        for (int i = 0; i < n; i++) {
            heap.push({nums[i][0], {i, 0}});
            max_value = max(max_value, nums[i][0]);
        }
        while (!heap.empty()) {
            auto top_value = heap.top();
            heap.pop();
            int dis = max_value - top_value.first;
            if (dis < res || (dis == res && res != INT_MAX && top_value.first < ans[0])) {
                res = dis;
                ans[0] = top_value.first;
                ans[1] = max_value;
            }
            int a = top_value.second.first;
            int b = top_value.second.second;
            if (b + 1 >= nums[a].size()) {
                break;
            }
            if (nums[a][b + 1] > max_value) {
                max_value = nums[a][b + 1];
            }
            heap.push({nums[a][b + 1], {a, b + 1}});
        }
        return ans;
    }
};