动态规划困难问题合集

dp可以用来解决有限集合的最值问题(max,min,count…)
dp问题分为两个部分

状态表示
状态计算

初始化和边界符合定义就可以

两个子序列的最大点积(190周赛)
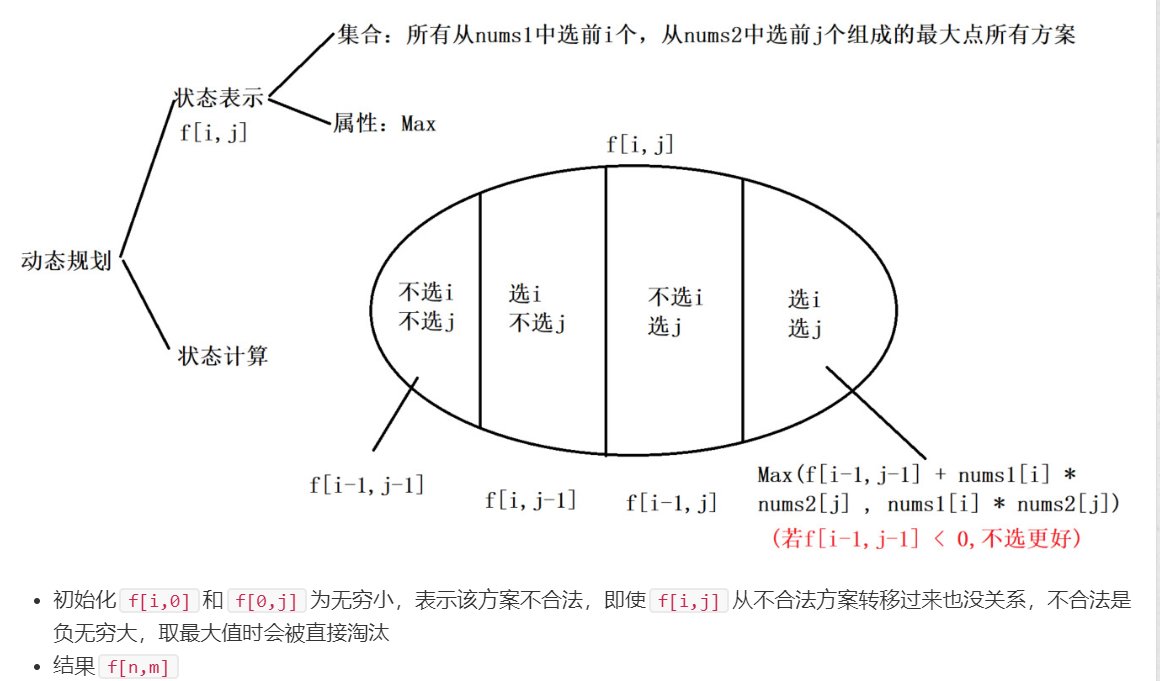
dp[i][j]的含义是到nums1[i]和nums2[j]为止的子序列的最大点积。
1.选择nums1[i]和nums2[j]

不选择前面的 dp[i][j]=nums1[i] $\times$ nums2[j]
也选择前面的 dp[i][j]=max(dp[i][j],nums1[i] $\times$ nums2[j]+dp[i-1][j-1])
因为dp[i][j]是截止到nums1[i]和nums2[j]中的最大点积，所以只需要dp[i-1][j-1]就可以了
事实上从这里可以看出想法一就是想法二的情况之一
2.选择nums1[i],不选择nums2[j]
这种情况很容易想到就用dp[i][j-1]来表示，但实际上dp[i][j-1]并不只表示这种情况，因为dp[i][j-1]表示的是到i和j-1为止的最大点击，nums[i]不一定就选，但是这个并不影响最终结果，因为我们是求最大值，当这个状态表示的集合多的时候，不会漏掉最大值的。
dp[i][j]=max(dp[i][j],dp[i][j-1])
3.不选择nums1[i],选择nums2[j]

等价于dp[i-1][j]
dp[i][j]=max(dp[i][j],dp[i-1][j])

4.nums1[i]，nums2[i]都不选。
这种情况包括在第二三种情况了

这样会保证两个序列长度相等吗?
会的，因为每次我们选取的操作–nums1[i] $\times$ nums2[j]+dp[i-1][j-1]，都是同时选取每一个序列的一个元素.

时间复杂度 $O(mn)$

c++

class Solution {
public:
    int maxDotProduct(vector<int>& nums1, vector<int>& nums2) {
        int n=nums1.size();
        int m=nums2.size();
        vector<vector<int>>dp(n+1,vector<int>(m+1,-0x3f3f3f));
        for(int i=1;i<n+1;i++)
            for(int j=1;j<m+1;j++){
                dp[i][j]=max(dp[i-1][j],dp[i][j-1]);
                dp[i][j]=max(dp[i-1][j-1]+nums1[i-1]*nums2[j-1],dp[i][j]);
                dp[i][j]=max(nums1[i-1]*nums2[j-1],dp[i][j]);
            }
        return dp[n][m];
    }
};

最长公共子序列

c++

class Solution {
public:
    int longestCommonSubsequence(string text1, string text2) {
        int p = text1.size();
        int q = text2.size();
        vector<vector<int>> dp(p+1,vector<int>(q+1,0));
        for(int i=1;i<p+1;i++)
            for(int j = 1;j<q+1;j++)
            {
                if(text1[i-1]==text2[j-1])
                    dp[i][j]=dp[i-1][j-1]+1;
                else
                    dp[i][j]=max(dp[i-1][j],dp[i][j-1]);
            }
        return dp[p][q];
    }
};

这道题到不算dp，也是用dp的一点思想来递归。
在第一层可以摆出6个ABA类型的和6个ABC类型的涂法。对于下面每一层，每一个ABA涂法可以拼接2个ABC涂法和3个ABA涂法，每一个ABC涂法可以拼接2个ABC涂法和2个ABA涂法。这样迭代可以算出第N层有几种ABA涂法和ABC涂法，相加就是答案。

c++

class Solution {
public:
    int numOfWays(int n) {
        long long aba = 6, abc = 6;
        const int m = pow(10,9) + 7;
        for(int i=1;i<n;i++){
            int ABA,ABC;
            ABA=(abc*2+aba*3)%m;
            ABC=(abc*2+aba*2)%m;
            abc=ABC,aba=ABA;
        }
        return (abc+aba)%m;
    }
};