简介

k-means algorithm算法是一个聚类算法，把n的对象根据他们的属性分为k个分割，k < n。假设对象属性来自于空间向量，并且目标是使各个群组内部的均方误差总和最小。通过迭代的方式将样本分到K个簇。

基本方法

选取K个点做为初始聚集的簇心（也可选择非样本点）;
分别计算每个样本点到 K个簇核心的距离（这里的距离一般取欧氏距离或余弦距离），找到离该点最近的簇核心，将它归属到对应的簇；
所有点都归属到簇之后， M个点就分为了 K个簇。之后重新计算每个簇的重心（平均距离中心），将其定为新的“簇核心”；
反复迭代 2 - 3 步骤，直到达到某个中止条件

sklearn实现

python

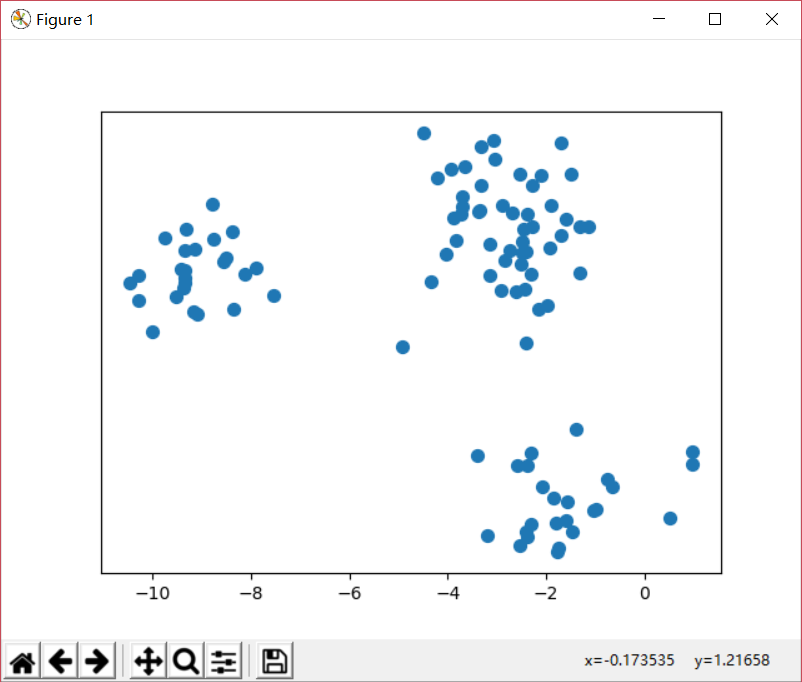
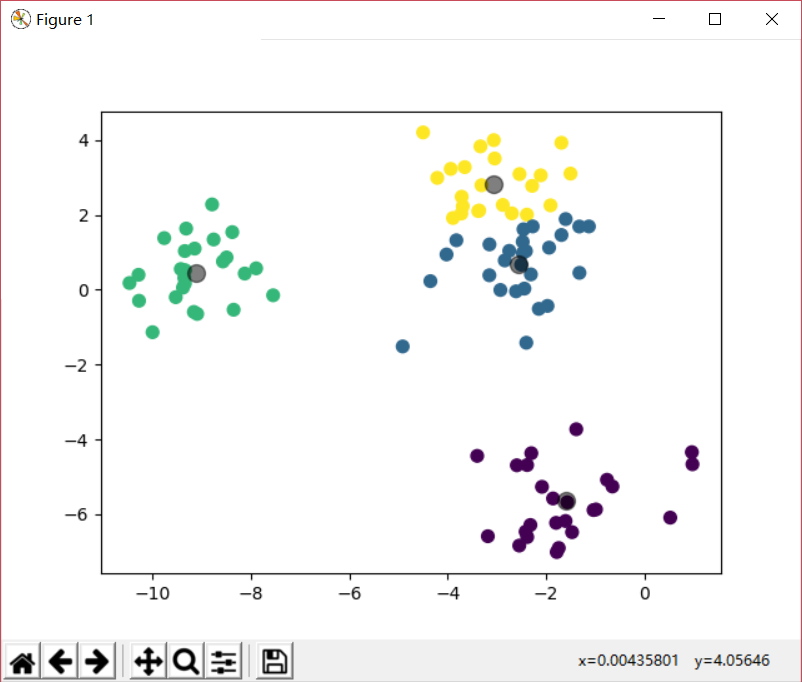
import matplotlib.pyplot as plt
from sklearn.datasets import make_blobs
from sklearn.cluster import KMeans

#产生数据
k=4
X,Y = make_blobs(n_samples=100, n_features=2, centers=k)


#构建模型
km = KMeans(n_clusters=k, init='k-means++', max_iter=300)
km.fit(X)

# 获取簇心
centroids = km.cluster_centers_
# 获取归集后的样本所属簇对应值
y_kmean = km.predict(X)
print(y_kmean)
# 呈现未归集前的数据
plt.scatter(X[:, 0], X[:, 1], s=50)
plt.yticks(())
plt.show()

plt.scatter(X[:, 0], X[:, 1], c=y_kmean, s=50, cmap='viridis')
plt.scatter(centroids[:, 0], centroids[:, 1], c='black', s=100, alpha=0.5)
plt.show()

手工实现

python

import numpy as np
from sklearn.datasets import make_blobs
from math import sqrt
import random
import matplotlib.pyplot as plt
from scipy import spatial

#产生数据
k=4
X,Y = make_blobs(n_samples=100, n_features=2, centers=k)
def calcuDistance(vec1, vec2):
    # 步骤1：定义欧式距离的公式
    # 计算两个向量之间的欧式距离：根号下[(x_1-x_2)^2+(y_1-y_2)^2+...+(x_n-y_n)^2]
    # ver1 - ver2：表示两个向量的对应元素相减
    return np.sqrt(np.sum(np.square(vec1 - vec2)))  #注意这里的减号

def k_means(data,k,Y):
    m, n = data.shape # m：样本数量，n：每个样本的属性值个数
    cores = data[np.random.choice(np.arange(m), k, replace=False)] # 从m个数据样本中不重复地随机选择k个样本作为质心
    print(cores)

    while True: # 迭代计算
        #d = np.square(np.repeat(data, k, axis=0).reshape(m, k, n) - cores)
        #distance = np.sqrt(np.sum(d, axis=2)) # ndarray(m, k)，每个样本距离k个质心的距离，共有m行
        distance = spatial.distance.cdist(data, cores,metric='euclidean')
        index_min = np.argmin(distance, axis=1) # 每个样本距离最近的质心索引序号
        
        if (index_min == Y).all(): # 如果样本聚类没有改变
            return Y, cores # 则返回聚类结果和质心数据
        
        Y[:] = index_min # 重新分类
        for i in range(k): # 遍历质心集
            items = Y==i # 找出对应当前质心的子样本集 ，对应的items为[True,false......]
            cores[i] = np.mean(data[items], axis=0) # 以子样本集的均值作为当前质心的位置



 
result,cores=k_means(X,k,Y)
plt.scatter(X[:, 0], X[:, 1], s=50)
plt.yticks(())
plt.show()
print(Y)
plt.scatter(X[:, 0], X[:, 1], c=Y, s=50, cmap='viridis')
plt.scatter(cores[:, 0], cores[:, 1], c='black', s=100, alpha=0.5)
plt.show()

k-means的改进

k-means改进的一个路线就是尽可能加快收敛速度，这个方向有几个思路：
1.质心初始化：选择初始质心之间有一些策略比如尽量远离，有助于反应数据的分布，加快收敛。
2.改进k-means的迭代过程，有几个方向，一个改进复杂度，比如数据的访问用KD树来索引，一个是改进目标函数（原始目标函数就是使同一类的离质心距离最小），有一个思路是时刻更新质心，比如移动一个样本到最近的类别，就立刻更新相应的两个类质心，这样改变了每轮都要对所有样本更新label的繁琐过程。