激活函数（Activation functions）

如果不使用激活函数，无论神经网络多少层都会是个线性激活函数

最基本的线性回归函数，一般用在最后一层。
除了二分类问题，不要使用sigmoid，tanh变现总是更好，但这些函数当z很大时，梯度会很小，训练会很慢，所以推荐relu函数。
ReLu函数只要 $z$ 是正值的情况下，导数恒等于1，当是 $z$ 负值的时候，导数恒等于0。从实际上来说，当使用的导数时， $z$ =0的导数是没有定义的。但是当编程实现的时候， $z$ 的取值刚好等于0.00000001，这个值相当小，所以，在实践中，不需要担心这个值， $z$ 是等于0的时候，假设一个导数是1或者0效果都可以。这里也有另一个版本的Relu被称为Leaky Relu,这个函数通常比Relu激活函数效果要好，尽管在实际中Leaky ReLu使用的并不多.

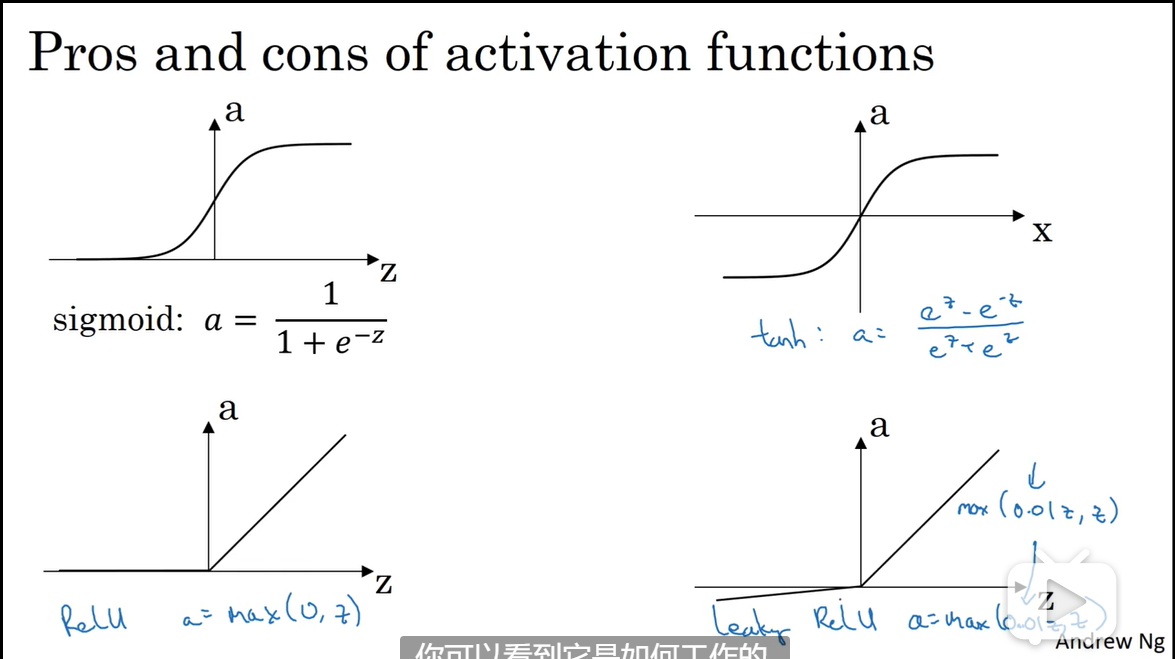
对于sigmoid函数 $g(z)=\frac{1}{1+e^{-x}}$ ,他的导数等于 $g(z)\times (1-g(z))$
对于tanh函数 $\frac{e^{x}-e^{-x}}{e^{x}+e^{-x}}$ ,他的导数等于 $1-(tanh(z))^{2}$
Relu函数 $g(z)=max(0,z)$ ,leaky Relu函数 $g(z)=max(0.01z,z)$

下限为0，无上限
严格递增
sparse activation
softmax也可以当作激活函数来看，用在分类问题

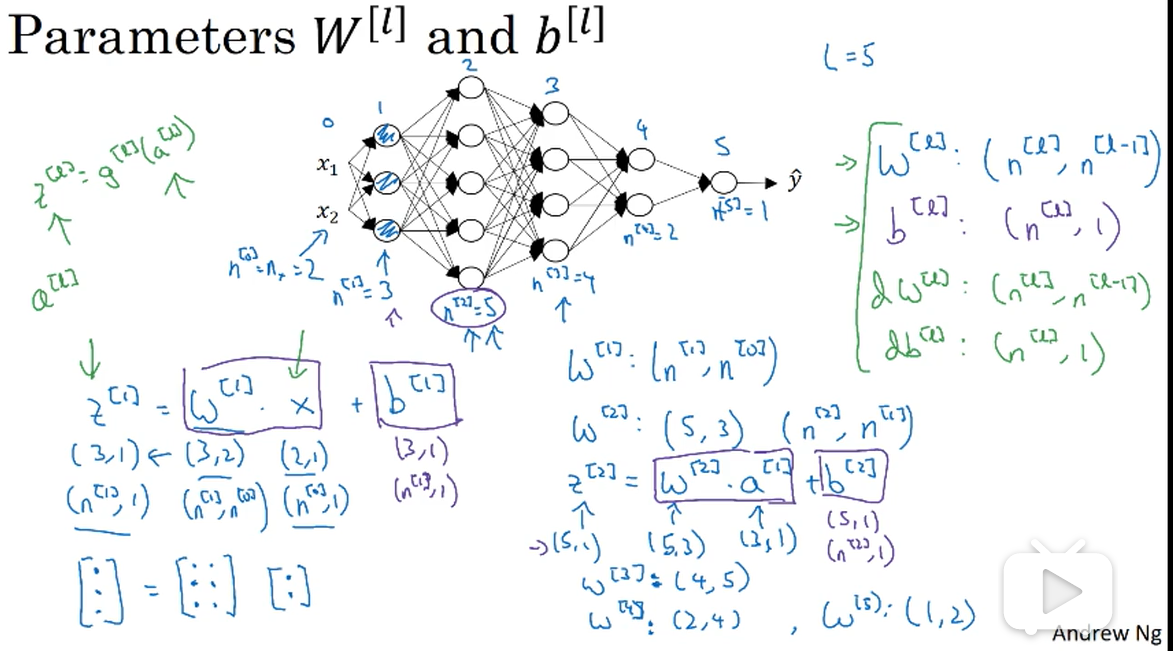
矩阵的维数

比如图中的神经网络，第一个隐藏层 $z^{[1]}=w^{[1]}x+b^{[1]}$ , $z^{[1]}$ 是3×1的矩阵， $x$ 是2×1的矩阵，所以 $w^{[1]}$ 是3×2的，总结起来就是 $w^{[L]}$ 是 $n^{[L]}\times n^{[L-1]}$ 的，对 $dw$ 也是一样的， $b^{[L]}$ 就是 $n^{[L]}\times1$ 的，见图片右半部分

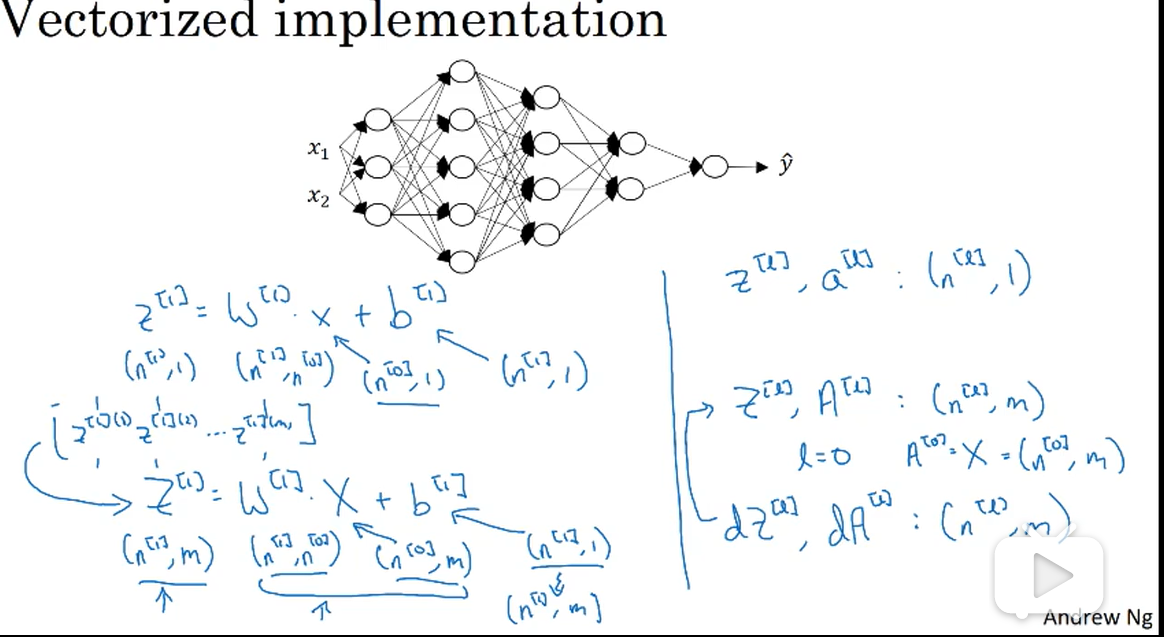
之后可以将 $z^{[1]}$ 叠加起来，m为样本数量

参数随机初始化（Random+Initialization）

$W^{[1]}=np.random.rando(2,2) \cdot 0.01,b=np.zeros((2,1))$
为什么是0.01，而不是100或者1000。我们通常倾向于初始化为很小的随机数。因为如果你用tanh或者sigmoid激活函数，或者说只在输出层有一个Sigmoid，如果 $W$ 很大， $Z$ 就会很大或者很小，因此这种情况下你很可能停在tanh/sigmoid函数的平坦的地方(见图3.8.2)，这些地方梯度很小也就意味着梯度下降会很慢，因此学习也就很慢。

正则化（Regularization）

1.为什么只正则化参数 $w$ ？为什么不再加上参数 $b$ 呢？你可以这么做，只是我习惯省略不写，因为通常是一个高维参数矢量，已经可以表达高偏差问题，可能包含有很多参数，我们不可能拟合所有参数，而 $b$ 只是单个数字，所以 $w$ 几乎涵盖所有参数，而不是 $b$ ，如果加了参数 $b$ ，其实也没太大影响，因为只是众多参数中的一个，所以我通常省略不计，如果你想加上这个参数，完全没问题。

2.为什么正则化会有用？当 $\lambda$ 增大， $w$ 接近于0，会减少很多隐藏单元的影响，网络会变得简单，接近于逻辑回归， $z$ 也会很小( $z^{[l]}=w^{[l]}a^{[l-1]}+b^{[l]}$ ),会呈线性。
3.其他正则化方法：数据扩增（比如图片翻转、裁剪、扭曲），early stop

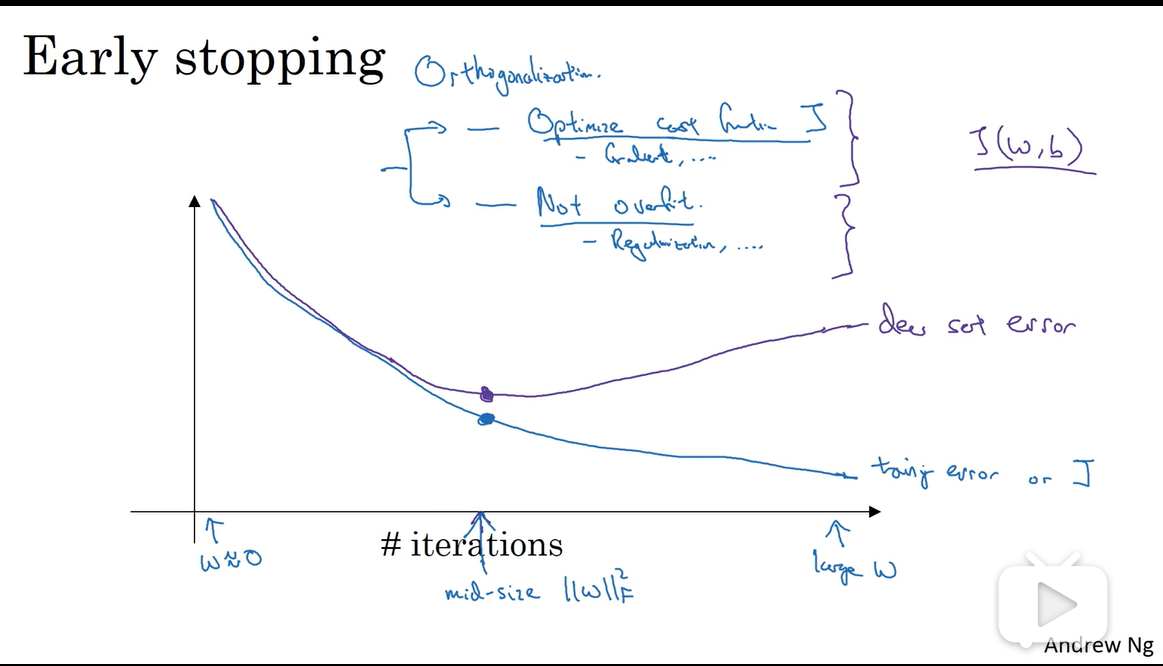
early stop无法将降低损失函数和过拟合独立处理，会很复杂，所以更倾向L2正则化，虽然要尝试很多不同的 $\lambda$ ，计算代价会很大

归一化

为什么要归一化？代价函数看起来会更对称，无论从哪个位置开始都能更直接的找到最小值，可以使用较大的步长。

padding

普通的卷积两个缺点，第一个缺点是每次做卷积操作，你的图像就会缩小，从6×6缩小到4×4，你可能做了几次之后，你的图像就会变得很小了，可能会缩小到只有1×1的大小。你可不想让你的图像在每次识别边缘或其他特征时都缩小，这就是第一个缺点。第二个缺点时，如果你注意角落边缘的像素，这个像素点只被一个输出所触碰或者使用，因为它位于这个3×3的区域的一角。但如果是在中间的像素点，就会有许多3×3的区域与之重叠。所以那些在角落或者边缘区域的像素点在输出中采用较少，意味着你丢掉了图像边缘位置的许多信息。
对于 $N \times N/$ 的图像， $f \times f$ 的filter（通常为奇数），paddy为p，步长stride为2，最后得到的矩阵为 $[\frac{n+2p-f}{s}+1] \times [\frac{n+2p-f}{s}+1]$ ,如果这个不是整数，我们向下取整，

损失函数

$argmin \frac{1}{T}\sum_{t}^{}L(f(x^{(t)};\theta ),y^{(t)})+\lambda \Omega (\theta )$