The web as a graph

pagerank是谷歌用来计算网页重要性的算法，我们把网页想象成节点，超链接想象成边，这就形成了一张有向图。
当然我们只考虑静态网页，不考虑防火墙拦截、无法访问这些情况。

两种有向图：
1.强连通图Strongly connected graphs：任意节点可以到达任意节点。
2.有向无环图Directed Acyclic Graph (DAG):首先没有环，u能达到v，但v不能达到u。
求strongly connected components (SCCs):对给定节点分别求入度和出度的BFS,然后对两个集合求交集

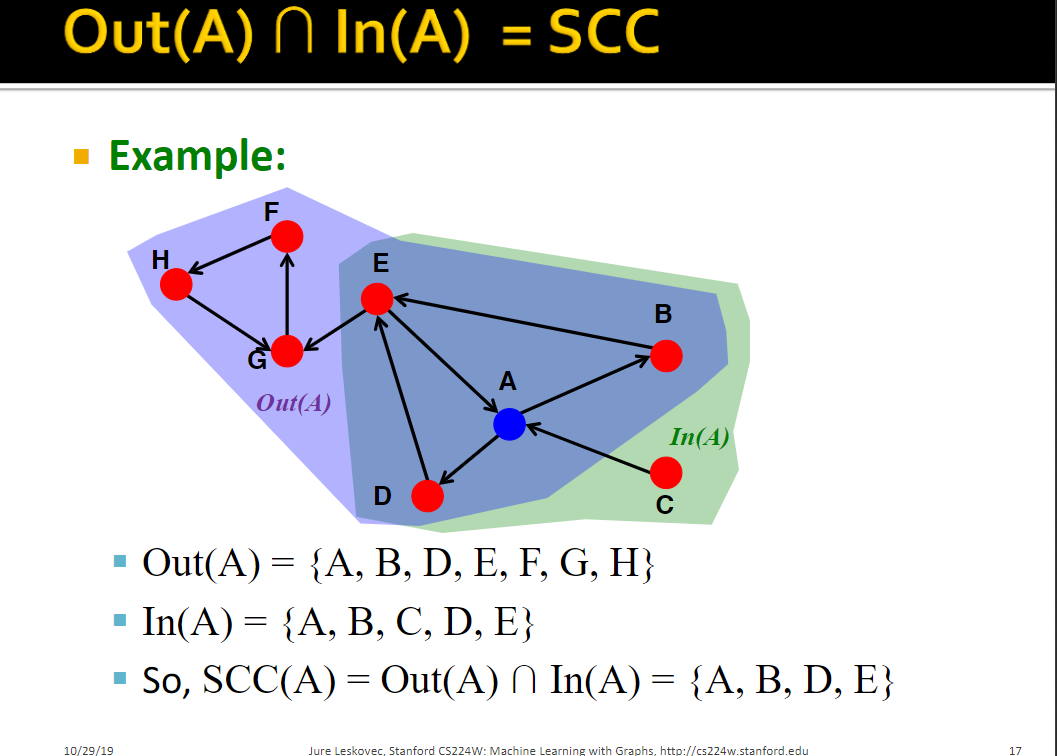
Bowtie structure of the web graph

Broder et al. (1999) took a large snapshot of the web and tried to understand how the SCCs in the web graph fit together as a DAG
这张图Here the starting nodes are sorted by the number of nodes that BFS visits when starting from that node

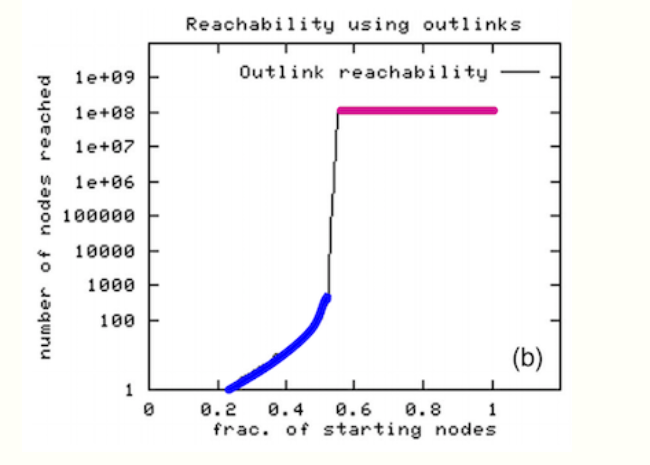
图中蓝色节点只能访问一小部分节点，紫红色节点可以访问很多节点
通过这个我们可以得出网络中的图组成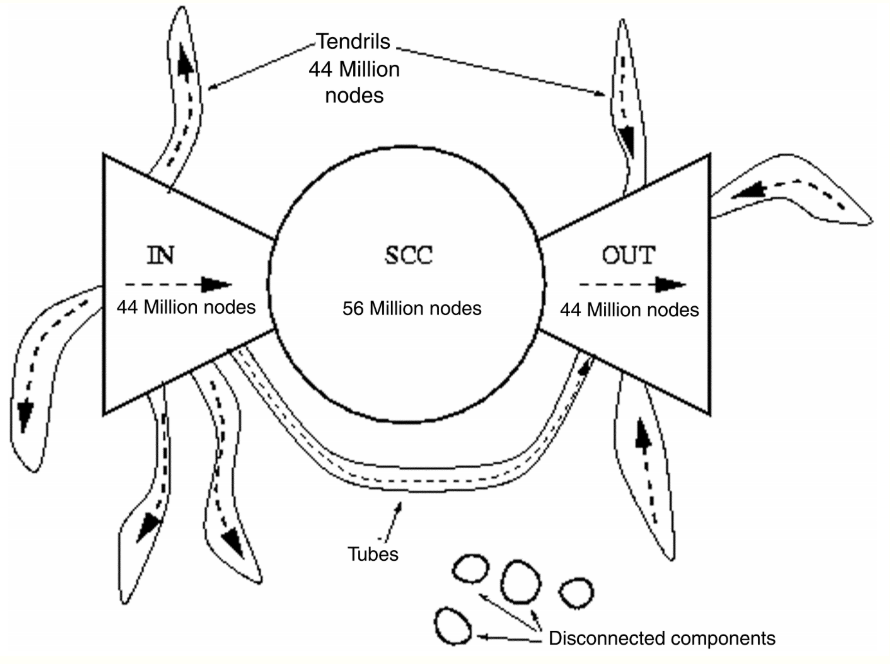

PageRank - Ranking nodes on the graph

核心想法是吧links当作votes，一个节点的重要性是由被所指向的其他节点决定的

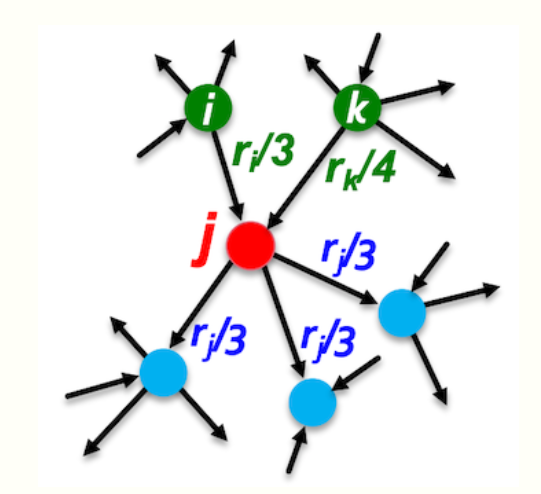
公式为 $r_{j}= \sum _ {i \rightarrow j}\frac{r_{i}}{d_{i}}$

Matrix formulation

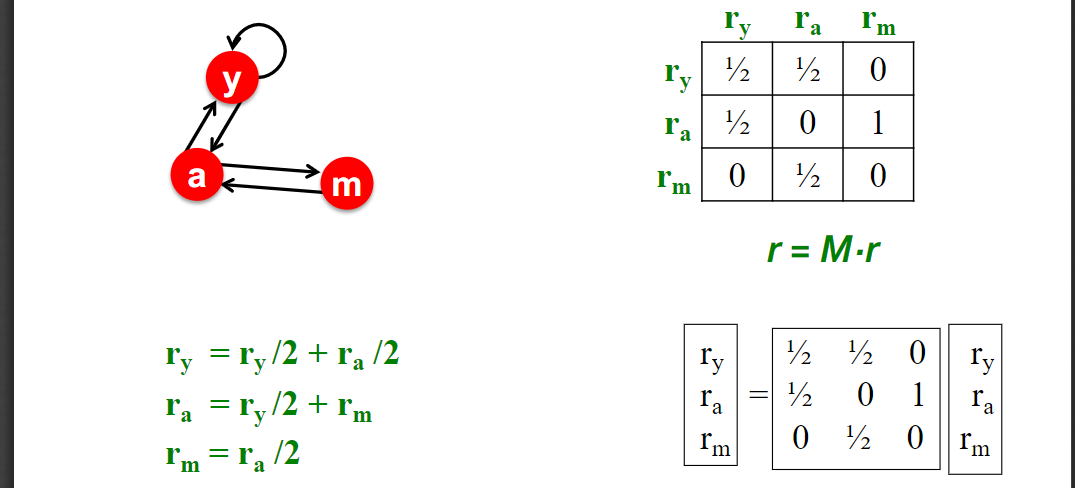
这种计算方法需要N个式子，需要很长的时间。所以我们用邻接矩阵M来代替，M的每个列的和为1 $if j \rightarrow i,then W_{^{ij}}=\frac{1}{d_{j}}$ ,则 $r=Mr$ ，如下图的计算过程

之后进行不断地迭代， $M(M...(M(Mr)$ 直到 $|r-r^{'}|< \varepsilon$

PageRank: Problems

1.dead ends:没有out-links

2.Spider traps：节点发出的边只有自环，最终会吸收所有的重要性，比如图中b会聚集所有的重要性，a会没有重要性

解决方法是random teleportation或者random jumps

当一次随机游走完成，下次网上冲浪有两种选择，有概率 $\beta$ 跟随link， $1-\beta$ 跳到其它网页,跳到其他的网页节点有相同的可能性， $\beta$ 通常设定在0.8到0.9
综合起来就是: $r_{j}= \sum _ {i\rightarrow j}\frac{r_{i}}{d_{i}}+(1-\beta )\frac{1}{N}$
下面可以定义谷歌矩阵 $A= \beta \times M+(1-\beta )[\frac{1}{N}]_ {N \times N}$ ， $r=A \times r$
注意这个公式假设M没有dead ends。我们可以提前处理矩阵M去除dead ends或者使用概率为1的随机random teleports

Computing PageRank: Sparse matrix formulation

但是这样对于节点太多的话，存储矩阵 $A(N\times N)$ 需要大量的空间，我们可以这样来计算： $r=\beta M \times r+\frac{1-\beta }{N}$ , $\frac{1-\beta }{N}$ 是一个向量，因为这样M是个稀疏矩阵，与向量乘机就没有那么大的计算量了

下面给出完整的算法流程