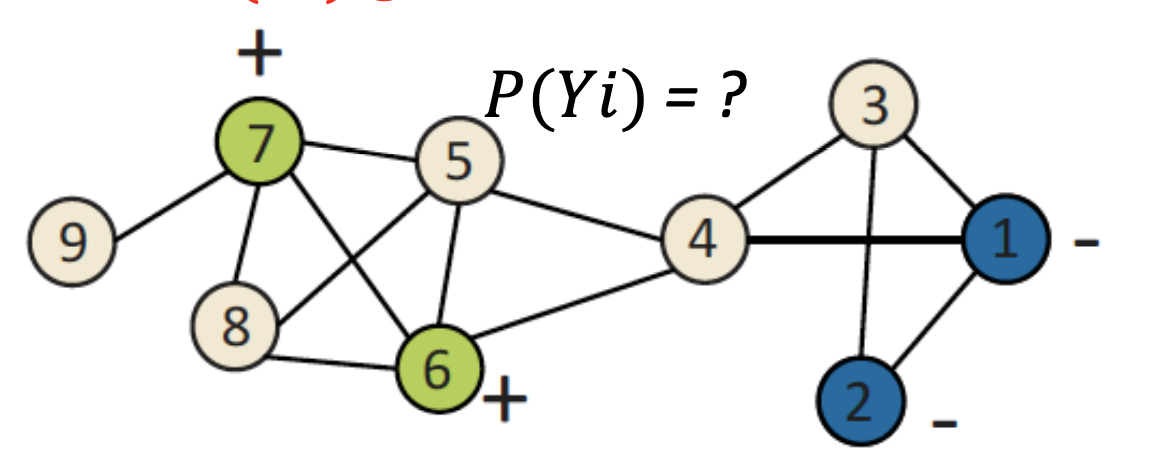
Node Classification

主要解决问题：给定一个网络，部分节点有标签，我们如何预测其它节点的标签。
例子：反欺诈案例，一些节点是欺诈者，一些节点是合法客户，我们怎么找到其它的欺诈者和合法客户。

补充：
图算法应用的任务有：

node focused，以节点为主体，预测节点的标签等，比如上面的反欺诈的例子；
edge focused，以边为主体，预测边的标签，比如推荐系统中用户与商品是否发生关联（即用户是否购买商品），对这种关联关系是否发生进行预测；
graph focused，以整个图为主题，预测图的标签等，比如化学分子的类别预测，整个化学分子是一副完整的图，其节点是不同的化学原子；

这节课主要讲节点分类的问题，也是目前图算法应用较多的领域，我们熟悉的gcn就是属于解决node focused任务的gnn的变体结构之一。
Collective Classification is an umbrella term describing how we assign labels to all nodes in the network together. We then propagate the information from these labels around the network and attempt to come up with stable assignments for each node. We are able to do these tasks because networks have special properties, specifically, correlations between nodes, that we can leverage to build our predictor. Essentially, collective classification relies on the Markov Assumption that the labely $Y_{i}$ of one node depends on the labels of its neighbors, which can be mathematically written as: $P(Y_{i}|i)=P(Y_{i}|N_{i})$

The three main techniques that are used are Relational Classification, Iterative Classification, and Belief Classification, roughly ordered byhow advanced these methods are.

Correlations in a Network

Homophily

Homophily generally refers to the tendency of individuals to associate and bond with similar others. Similarities, for instance in a social network, can include a variety of attributes, including age, gender, organizational affiliation, taste, and more.

Influence

Another example of why networks may demonstrate correlations is Influence. Under these circumstances, the links and edges formed can influence the behavior of the node itself

Confounding

Confounding variables can cause nodes to exhibit similar characteristics. For instance, the environment we are raised in may influence our similarity in multiple dimensions, from the language we speak, to our music tastes, to our political preferences.

collective classification

Whether or not a particular node X receives a particular label may depend on a variety of factors. In our context, those most commonly include:

未知样本的标签取决于：

这个未知样本O的特征；
这个未知样本O的相邻节点；
这个未知样本O的相邻节点的特征；

实际上如果仅仅考虑第一个条件就回到了我们传统的机器学习算法的范畴里了；
主要思想：
节点的标签是由其邻居的标签决定的
对于有标签的节点，就用ground-truth就好，没有标签的随机初始化，对于所有节点用随机的顺序更新直到收敛或者达到最大迭代次数

但是这种方法的问题在于：
1、无法保证一定能收敛（就是可能收敛也可能不收敛）（这里讲课的大佬给了一个经验法则，如果不收敛，但是随着时间的推移，不收敛的程度没有变大而是周期性的变动，那么这个时候我们也可以结束迭代）
2、模型仅仅使用的是节点的标签信息，但是没有用到节点的属性信息（特征）；

Iterative Classification

第一种方案 relational classifiers 仅仅根据标签进行迭代，完全浪费了节点的属性信息，显然如果节点之间的属性非常相似，那么节点的标签也很可能是一样的，所以iterative classification 的思路就是同时利用节点的属性（特征矩阵）和标签；

其过程是：

为每一个节点创建一个向量形式（这里的意思应该是根据每个节点的属性得到一个特征向量）
使用分类器对得到的特征矩阵结合标签进行训练；
对于一个标签可能拥有许多的邻居，因此我们可以对其邻居的节点进行各类统计指标的计算加入特征中作为衍生特征，例如count计数、mode 求众数、proportion求占比、均值、是否存在的bool特征等；

这里详细介绍了iterative classifiers的整个过程：
首先是bootstrap phase，先使用特征矩阵来训练一个传统的机器学习模型比如svm、knn，然后预测标签，还是伪标签的思路；
然后是iteration phase，进入迭代步骤，对于每一个节点i都重复：
1. 更新特征向量ai；
2. 重新训练并且预测得到新的标签yi

一直到预测的概率整体不再变化或者变动不大或是达到了最大迭代次数；
同样，收敛也是无法保证的。
（这里补充了一点使用的知识，就是这类迭代的算法怎么去确定其停止条件，一个就是输出的值的收敛，理想状态是输出基本不发生改变，如果始终不收敛就看输出的差值的波动情况，如果是周期性在某个范围内波动而其差值不随迭代次数继续增大则可以选择输出差值较低的结果作为最终的收敛状态；另一个思路就比较简单了，设定最大迭代次数）

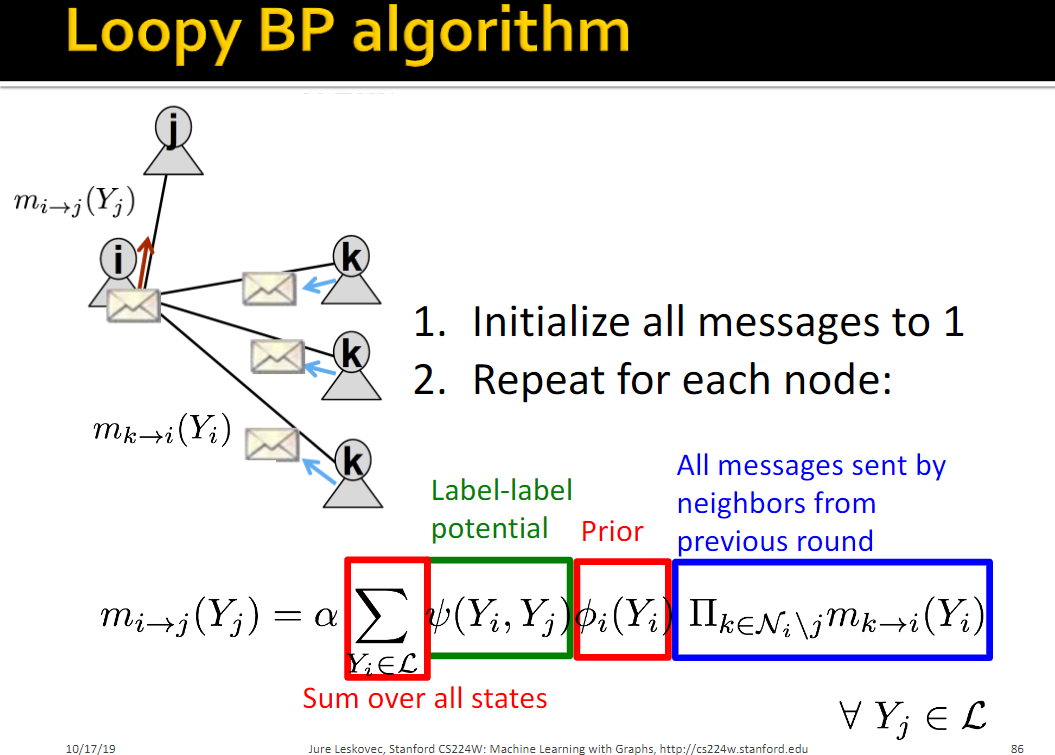
Message Passing/Belief Propagation

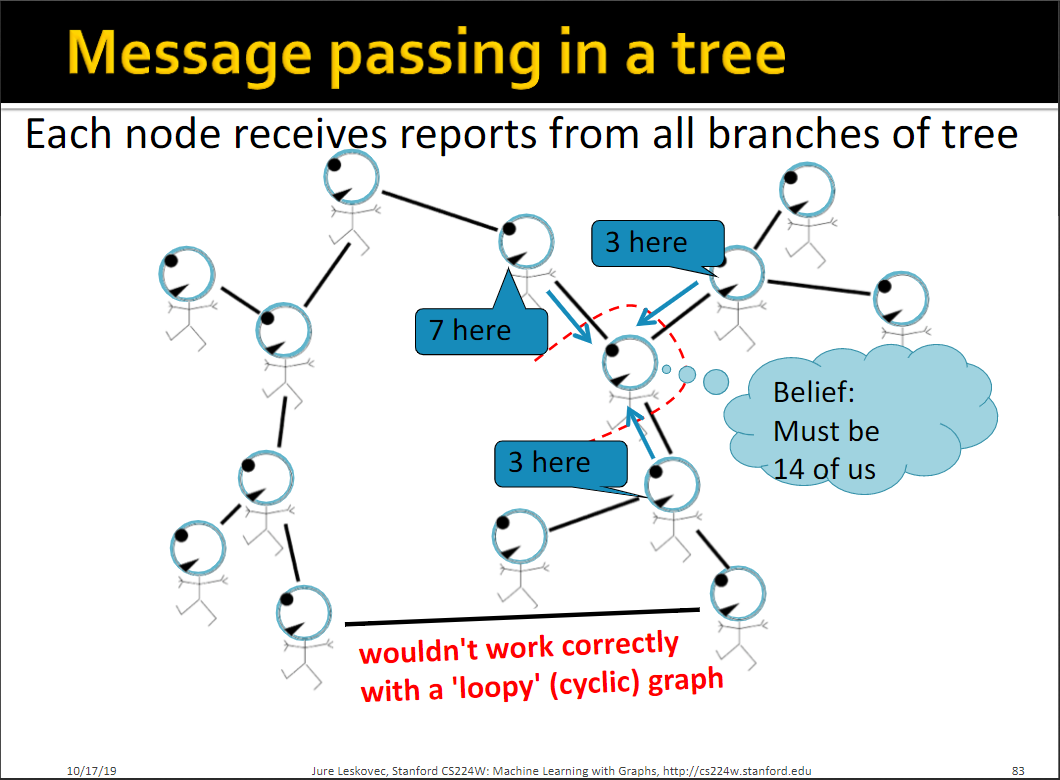
This equation summarizes our task: to calculate the message from i to j, we will sum over all of our states the label-label potential multiplied by our prior, multiplied by the product of all the messages sent by neighbors from the previous rounds. To initialize, we set all of our messages equal to 1. Then, we calculate our message from i to j, using the formula described above. We will repeat this for each node until we reach convergence, and then we can calculate our final assignment, i’s belief of being in state $Y_{i}$ or $b(Y_{i})$